35419
Matematika
Kvadratické rovnice
Riešenie rýdzo kvadratickej rovnice
Kvadratická rovnica bez linárneho člena - tzv. rýdzo kvadratická rovnica je rovnica v tvare
ax2 + c = 0,
kde a, c ∈ R - {0}.
Tento typ rovnice riešime rozkladom na súčin v závislosti od konkrétnych hodnôt koeficientov a, c. Prečo? Najlepšie to pochopíte na príkladoch.
Príklad 1:
Riešte v množine R rovnicu: x2 - 9 = 0.
Riešenie:
x2 - 9 = 0
je zrejmé, že rovnicu môžeme rozložiť na súčin podľa vzťahu a2-b2=(a-b)(a+b)
(x - 3) · (x + 3) = 0
⇒ x - 3 = 0 alebo x + 3 = 0
Po vyriešení oboch lineárnych rovníc
x - 3 = 0 / +3
x = 3x + 3 = 0 / -3
x = -3získame korene danej kvadratickej rovnice.Teda P = {-3, 3}.
Príklad 2:
Riešte v množine R rovnicu: -4x2 + 25 = 0.
Riešenie:
Riešime obdobne ako predošlý príklad - úpravou na súčin. Pre zjednodušenie môžeme vymeniť poradie kvadratického a absolútneho člena: 25 - 4x2 = 0.
(5 - 2x)(5 + 2x)=0
...
Teda P = {-2,5; 2,5}.
Na základe uvedených dvoch príkladov môžeme vysloviť záver:
Ak a<0 a b>0 alebo a>0 a b<0, tak daná rovnica má práve dva reálne korene.
Samozrejme, riešenie si môžeme aj urýchliť:
Príklad 3:
Riešte v množine R rovnicu: -4x2 + 16 = 0.
Riešenie:
-4x2 + 16 = 0 /-16
-4x2 = -16 /:(-4)
x2 = 4
x1, 2 = ±2Teda P = {-2; 2}.
Tento spôsob riešenia skrýva úskalie. Častou chybou je, že študent rieši rovnicu x2 = 4 iba odmocnením, čiže x = 4 = 2 a to je chyba.
Správne:
|x| = 4 = 2, čiže x1, 2 = ±2
Zostáva nám overiť už iba jediné - ak oba koeficienty a, c sú kladné (záporné) čísla.
Príklad 4:
Riešte v množine R rovnicu: -4x2 - 16 = 0.
Riešenie:
-4x2 - 16 = 0 /+16
-4x2 = +16 /:(-4)
x2 = -4Lenže druhá mocnina ľubovoľného reálneho čísla je vždy nezáporné číslo, čiže číslo ≥0, ale -4<0.
Daná rovnica teda nemá riešenie.
Teda P = {}.
K podobnému záveru ako v predošlom príklade by sme dospeli i pre kladné koeficienty a, c. Preto
Ak a<0 a b<0 alebo a>0 a b>0, tak daná rovnica nemá riešenie v obore reálnych čísel.
Riešenie kvadratickej rovnice
V predchádzajúcich článkoch sme si ukázali spôsob riešenia kvadratických rovníc, kde chýbal lineárny alebo absolútny člen, prípadne riešenie kvadratickej rovnice v normovanom tvare s využitím Vietovych vzorcov.
Čo ale v prípade, ak nemôžeme využiť ani jeden z predchádzajúcich spôsobov?
V takom prípade o riešiteľnosti danej kvadratickej rovnice ax2 + bx + c = 0 - či daná rovnica má alebo nemá riešenie, resp. aké sú hodnoty koreňov danej kvadratickej rovnice rozhoduje výraz
D = b2 - 4ac,
ktorý nazývame diskriminant.
Platí:
- ak D > 0, tak daná kvadratická rovnica má 2 rôzne reálne korene
- ak D = 0, tak daná kvadratická rovnica má dva rovnaké reálne korene, čiže tzv. dvojnásobný reálny koreň
- ak D < 0, tak daná kvadratická rovnica nemá riešenie v obore reálnych čísel (samozrejme v obore komplexnýxh čísel má dva imaginárne komplexne združené korene)
Z predchádzajúceho je zrejmé, že v prípade D≥0 má zmysel pokračovať v riešení kvadratickej rovnice.
Ako určíme korene x1, x2?
x1, 2 = -b ± D resp. x1, 2 = -b ± b2 - 4ac 2a 2a Príklad 1:
Riešte v množine R rovnicu: 5x2 - 2x - 3 = 0.
Riešenie:
D = b2 - 4ac = (-2)2 - 4·5·(-3) = 4 + 60 = 64
D > 0 ⇒ daná rovnica má dva rôzne reálne korene, ktoré vypočítame.
x1, 2 = -b ± D = -(-2) ± 64 = 2 ± 8 2a 2·5 2·5 Teda x1 = 2 + 8 = 1 a x2 = 2 - 8 = -6 = -3 2·5 2·5 10 5 P = {-3/5, 1}
Príklad 2:
Riešte v množine R rovnicu: 25x2 - 10x + 1 = 0.
Riešenie:
D = b2 - 4ac = (-10)2 - 4·25·1 = 100 - 100 = 0
D = 0 ⇒ daná rovnica má dvojnásobný reálny koreň, ktorý vypočítame.
x1, 2 = -b ± D = -(-10) ± 0 = 10 = 1 2a 2·25 50 5 P = {1/5}
Všimnite si:
Keď D=0, riešením je dvojnásobný koreň a v takom prípade (tí, ktorí ovládajú vzťah a2+2ab+b2=(a+b)2) nie je problém riešiť rovnicu úpravou podľa tohto vzťahu.
25x2 - 10x + 1 = 0
(5x - 1)2 = 0
5x - 1 = 0
5x = 1
x = 1/5
Príklad 3:
Riešte v množine R rovnicu: 2x2 - 2x + 3 = 0.
Riešenie:
D = b2 - 4ac = (-2)2 - 4·2·3 = 4 - 24 = -20
D < 0 ⇒ daná rovnica nemá v obore reálnych čísel riešenie.
P = {}
Korene kvadratickej rovnice a graf kvadratickej funkcie
Pravdepodobne ste si uvedomili, že pri načrtávaní grafu alebo určovaní vlastností kvadratickej funkcie sme zostávali (na Pohodovej matematike) pri určovaní priesečníka grafu kvadratickej funkcie s osou y, ale na priesečníky s osou x sme „akosi zabúdali“.
A dôvod?
Prozaický, pri určovaní priesečníkov paraboly so súradnicovou osou y potrebujeme vedieť riešiť kvadratickú rovnicu. Veď posúďte sami.
Daná je kvadratická funkcia f: y = ax2 + bx + c, kde a≠0.
Vieme, že priesečník grafu tejto funkcie s osou x má súradnice Px=[x,0], teda poznáme y-ovú súradnicu priesečníka.
Dosaďme ju do predpisu kvadratickej funkcie.
0 = ax2 + bx + c
Usmievate sa? Vidíte dobre - dostali sme kvadratickú rovnicu, ktorej vyriešením získame x-ovú súradnicu priesečníka grafu danej kvadratickej funkcie so súradnicovou osou x.
Príklad 1:
Určte priesečníky Px grafu kvadratickej funkcie na obrázku so súradnicovou osou x.
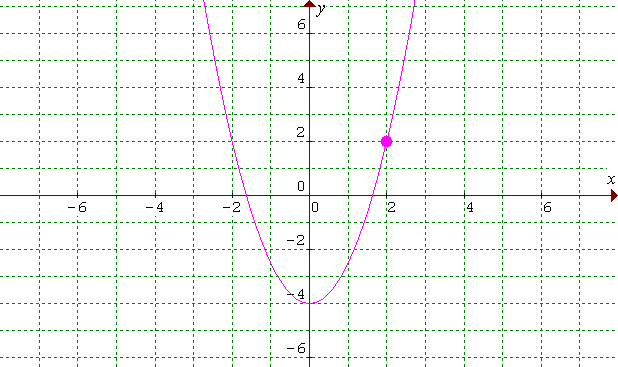
Riešenie:
Aby sme mohli určiť Px, potrebujeme poznať predpis kvadratickej funkcie, ktorej graf je na obrázku.
f: y = ax2 + bx + c
Z grafu vieme vyčítať: V=[0, -4], Py=[0,-4], bod [2,2]
Keďže Py=[0,-4], tak c = -4, teda f: y = ax2 + bx - 4
Keďže V=[0,-4], tak b = -4, keďže 0=-b/2a (bližšie pozri Kvadratická funkcia), teda f: y = ax2 - 4
Keďže poznáme bod [2, 2], tak jeho súradnice dosadíme do upraveného predpisu kvadratickej funkcie
y = ax2 - 4
2 = a·22 - 4 /+4
6 = 4a /:4
a = 1,5Poznáme teda predpis kvadratickej funkcie, ktorej graf je na obrázku:
f: y = 1,5x2 - 4
Px=[x, 0]
Dosadením do predpisu funkcie dostaneme: 0 = 1,5x2 - 4
Vyriešime danú kvadratickú rovnicu a získame jej korene: x1,2=± 2·2/3.
Px1 = [2·2/3, 0], Px2 = [-2·2/3, 0],